
As production increases, the minimum cost needed increases in a non-linear, exponential fashion, which makes sense given that Y (quantity produced) is in the numerator on the right-hand side of the cost function and positively related to the cost. Using the Cobb-Douglas production function and the cost minimization approach, we were able to find the optimal conditions for the cost function and plot the outcome relative to the quantity produced. The functional form of the CD production function:
PRODUCTION FUNCTION HOW TO
However, in this example, we will learn how to answer a minimization problem subject to (s.t.) the CD production function as a constraint. It is similarly used to describe utility maximization through the following function. Typical inputs include labor (L) and capital (K). The Cobb-Douglas (CD) production function is an economic production function with two or more variables (inputs) that describes the output of a firm. Appreciation goes out to the users who identified this error. Hence, I’ve updated the data frame used in the example to avoid this issue. Since the output of elasticity should be between the values of 0 and 1, this negative coefficient should not be possible. The beta coefficient generated a negative value which was used in the linear form of the Cobb-Douglass equation. In the previous example, I used R to generate a set of random numbers that were used in a regression model. The error was the negative value generated for the output elasticity of capital. But the change in output obtained by increasing the capital stock is lower when the capital stock is higher: this is the diminishing marginal product of capital.Update: This article was updated on 11 October 2021 when a user identified an error with the example used at the end.
As capital input is increased, output increases as well. This figure shows two properties of the aggregate production function. One reason is that we do not have a natural or an obvious measure for human capital, knowledge, or social infrastructure, whereas we do for labor and capital (hours of work and hours of capital usage).įigure 16.8 shows the relationship between output and capital, holding fixed the level of other inputs. In contrast to capital and labor, we do not assume that there are diminishing returns to human capital and technology.

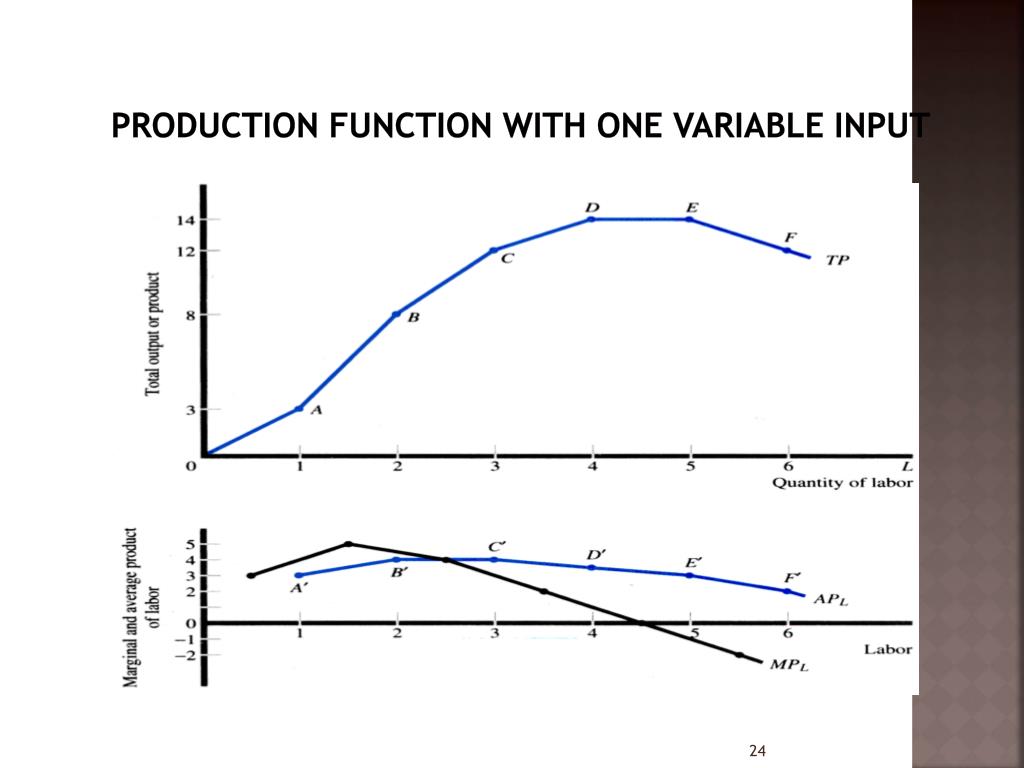
In addition, increases in output can also come from increases in human capital, knowledge, and social infrastructure. The more natural resources we have, the less additional output we obtain from additional resources.The more labor we have, the less additional output we obtain from additional labor.The more capital we have, the less additional output we obtain from additional capital.This is called diminishing marginal product. Second, the increase in output from adding more inputs is lower when we have more of a factor. In other words, the marginal products of these inputs are all positive. First, output increases when there are increases in physical capital, labor, and natural resources. The aggregate production function has several key properties. We group the inputs other than labor, physical, and human capital together, and call them technology. Anything else that we have not yet included.The amount of natural resources available in an economy.Social infrastructure-the general business, legal and cultural environment.Knowledge-basic scientific knowledge, and blueprints that describe the available production processes.Human capital-skills and education embodied in the workforce of the economy.



 0 kommentar(er)
0 kommentar(er)
